How Many Licks Does It Take to Get to the Center of a Tootsie Pop?

Today, tootsie pops are an internet phenomenon. Their brilliant marketing strategy along with tasty product fulfillment have led hundreds of articles to be published on the very topic of how many licks it takes to get to the center of a tootsie pop — one of their most successful advertising campaigns to date.

Some tootsie study groups handed out their pops left right and center, and had their team lick until they could lick no more. Other groups engineered interesting contraptions like artificial licking machines that resembled the human tongue for maximum accuracy. However, all of these studies suffered from a fatal flaw: sample size.

Presuming their approach was superior and none could compare, no group to-date has been clever enough to leverage their competitor’s data to maximize the accuracy of their hypothesis.

Until today.

What follows is a robust meta analysis of pre-existing tootsie pop studies by our highly scientific research group (me). We’ll conclude with an arithmetic average of the most probable number of licks, and finish this argument once and for all.

For maximum accuracy, we need to randomize our sample selection. To do so, we took the top 100 hits on Google for the term “How Many Licks Does It Take to Get to the Center of a Tootsie Pop” added their links to a Google Sheet, and then used a random sample function to draw 10.

In hindsight, we could have used their Google page rank as a trust factor in our later average to improve the representativeness of their lick number (LN), but we decided to keep things simple to streamline our study.

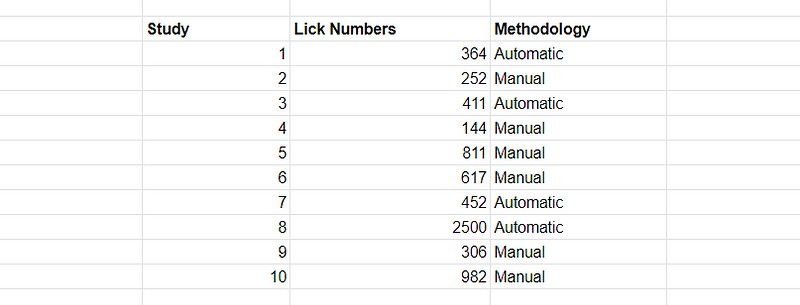
We thoroughly analyzed each of the ten articles, looking for important components of accuracy like their methodology, their sample size, the variability of their lick numbers, and so on. For any articles that had several LNs due to a multitude of different approaches, we performed a simple arithmetic average such that every article would be given just one lick number.

At this point, we had ten lick numbers categorized primarily by methodology (manual licking or automatic licking). We took a group-level arithmetic average and a total arithmetic average. The results are below.

Manual Licking Average: 519

Automatic Licking Average: 932

Total Average: 684

Notice the striking disparity between automatic and manual licking averages. This suggests that automatic licking machines are not as accurate as they might seem — there is a trade off between validity and ease of lick application.

Our approach details an exciting and novel statistical method of answering the question “how many licks does it take to get to the center of a tootsie pop”. Our methodology certainly could have been improved — for example, an increased sample size would have benefited the accuracy of the results — but we were limited primarily by our resources and the fact that I am just one man in his mother’s basement. More funding is needed.

Any future studies should include a more in-depth statistical analysis of results, as well as better writing and editing of the sequential paper.

There you have it. A robust, mathematical answer to the long-asked question of how many licks it takes to get to the center of a tootsie pop.

It’s not rocket science, folks. It’s statistics. Which is way harder.