A useful mental model I've been using to guide my entrepreneurial decisions recently is expected value (EV).
For those of you unfamiliar, EV is a concept in statistics whereby you take the probabilities of a set of events, and multiply them by their likelihoods, to get the expected result.
A more practical way to look at it—and the way that I personally employ EV—is the formula below.
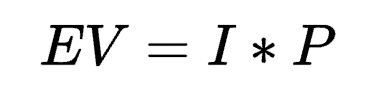
In plain English, this means that the expected value of a decision (EV) is equal to its impact (I) and the likelihood that you're successful at it (P).
EV is an extremely powerful framework to guide business decisions. I use it every day. Let's look at an example.
A night at the casino
One fine evening, you find yourself at a casino. You like dice games, and peruse the available options. As you walk around the tables, you notice one that looks interesting.
This dice game has a simple rule: if you roll a 4 or higher, you will make $100. However, to play this game, you need to "buy in" for $45.
Here's a simple question: is this game worth playing?
If you think about it logically, a die has six outcomes. You can roll a 1, 2, 3, 4, 5, or 6. So rolling "a four or higher" represents half of all possible options. Put another way, you have a 50% chance of making $100 every game.
That's where EV comes in. It lets us mathematically determine whether or not a 50% chance of winning $100 is worth $45.
Using our formula, we'd set the potential "impact" of each game to $100, and your chances of winning to 50%. Thus:
EV = $100 x 50%
EV = $50
In simple terms, that means the expected value of playing the game is $50. So if the cost is less than $50, then it's worth it to play the game. You're essentially making $5 every run.
Note: the first few times you play, you may very well run at a deficit. It's entirely possible that you lose 4 games in a row before you win. But in the long run, if you play consistently, your wins and losses will average out, and you will make consistent 10% returns on this game.
How EV applies to business
That was a pretty contrived example, I know. But I think about all of my entrepreneurial pursuits in a similar fashion.
If EV = impact x probability of success, then it seems to me that the optimal way to maximize the value of each decision I make is by looking at what makes the biggest splash, and then scaling it by how good I am (or how likely I am to succeed) at that particular thing.
Since we're talking about business, the "impact" here is usually a dollar figure. And when you frame things in that way, you'll quickly find you can use EV for any decision, small or large.
Applying this to a few real situations:
1. How to choose what to to work on today
Many people often spend several hours of their day floundering or focusing on relatively low-ROI actions. But if you approach your daily regimen using EV, it gets a lot simpler, and it lets you focus on the actions that live at the intersection of (impact) x (probability of success).
For instance, let's say you're working on your marketing. What's more impactful: a print media campaign to an established audience, or a new SEO campaign to an unknown audience?
Let's pretend that, somehow, you know the first option will make you $20,000, and since you've done it before, you also know your odds of success are somewhere around 80%.
Let's say the second option has an estimated gain of $100,000, but since you've never done it before, your odds of success are somewhere around 10%.
The EVs of these actions work out to $16K vs $10K. Meaning the print media campaign—a known quantity that may pay less up front, but that you're better at—is obviously the right choice if your goal is maximizing revenue.
It's obviously impossible to estimate exactly how much money you stand to make by choosing a particular action. But the precise amount isn't really the point. The very act of working through the EV calculation in your head is enough to help you prioritize and make better decisions.
2. What company to start
Maybe you want to start a new venture, but are at a crossroads of what to do next. You have a few candidate options and are looking at what to go all in on. We can solve this with EV.
- Starting the next social network a la Facebook. Companies like this have huge potential impacts (let's say $10B lifetime) but also very low odds of success (maybe 0.01%). If we do the math, $10B x 0.01% = $1,000,000.
- Starting a boutique marketing agency. Low potential impact (let's say $8M lifetime), but reasonably high odds of success (maybe 15%). If we do the math, $8M x 15% = $1,200,000.
I use these two diametrically opposed examples to illustrate a common problem I see novice entrepreneurs succumbing to: optimizing for the wrong thing. For instance, if what you care about is money (like most of us), it probably makes more sense to start a marketing agency than to play with extremely long odds of building a unicorn social network.
There are obviously many more variables here to consider—lifestyle, legacy, etc. But EV is a good way to cut through the noise and look at what you care about pragmatically. It forces your options to live on the same, level playing ground, and helps you eliminate what isn't important.
3. Whether to scale up or not
I bring up a marketing example again because adept marketers are professionals at using EV, and it drives a lot of their decision making.
In this example, let's say you're marketing for a company that sells shoes on the internet.
To start, you run an ad campaign which yields you a cost per click of $5.45. On average, it takes you ten clicks to get one conversion, so $5.45 x 10 = $54.50. Put another way, it costs you $54.50 to sell one of your shoes.
Let's say you sell each shoe for $150, and after shipping, handling, and other operational costs, each shoe sale nets you $50.00 before advertising spend.
Does it make sense to keep the campaign running?
Clearly, you're losing $50 - $54.50 = -$4.50 per shoe at face value. But here's where EV comes in.
Some customers purchase from the same store more than once. In practice, what this means is that one in every ten or fifteen people buy an extra pair of shoes from you over their lifetime, and a small minority (maybe one in a couple hundred) buy three or more.
You can frame this as an EV calculation. In reality it's as arbitrarily complex as you want, but here's a simple example that segments by purchase numbers up to three, assuming 12% of customers buy two shoes, and 0.5% of customers buy three:
- EV of a customer who buys once = $50 * 100%
- EV of a customer who buys twice = $100 * 12%
- EV of a customer who buys three times = $150 * 0.5%
Summing all of these EVs up would yield us $50 + $12 + $7.5 = $69.50.
Since $69.50 - $54.50 = $15.00, you're now "making" $15 per customer. What this means in practice is that as long as you have capital to deploy, and you're confident in your math, you will eventually produce a sizeable profit operating this campaign.
There are other factors as well—referral multipliers, for instance. Some people will love your shoes so much they'll rave about it to their friends, who will inevitably have some small chance of purchasing one themselves. Since you didn't spend ad money on acquiring that referral, you can add it to the EV summation we calculated previously.
Closing
If you've been to college or university, you'll have invariably read about EV in a your average entry level statistics textbook.
But the utility is often lost on students. Its real value isn't in calculating dry probability problems, or solving fake dice roll games—it's on optimizing your day-to-day entrepreneurial tasks to make more money, and giving you a simple mental model by which to compare larger decisions.
This is why I chose to start focusing on building a brand, by the way. The potential impact was large, and I rated the probability of success as reasonably high. Compared to my other options, this one had a much higher EV.
What high EV decisions are you not taking advantage of in your life?






